Local Topology Measures of Contextual Language Model Latent Spaces With Applications to Dialogue Term Extraction
[Benjamin Ruppik, Michael Heck, Carel van Niekerk, Renato Vukovic, Hsien-chin Lin, Shutong Feng, Marcus Zibrowius, Milica Gašić]
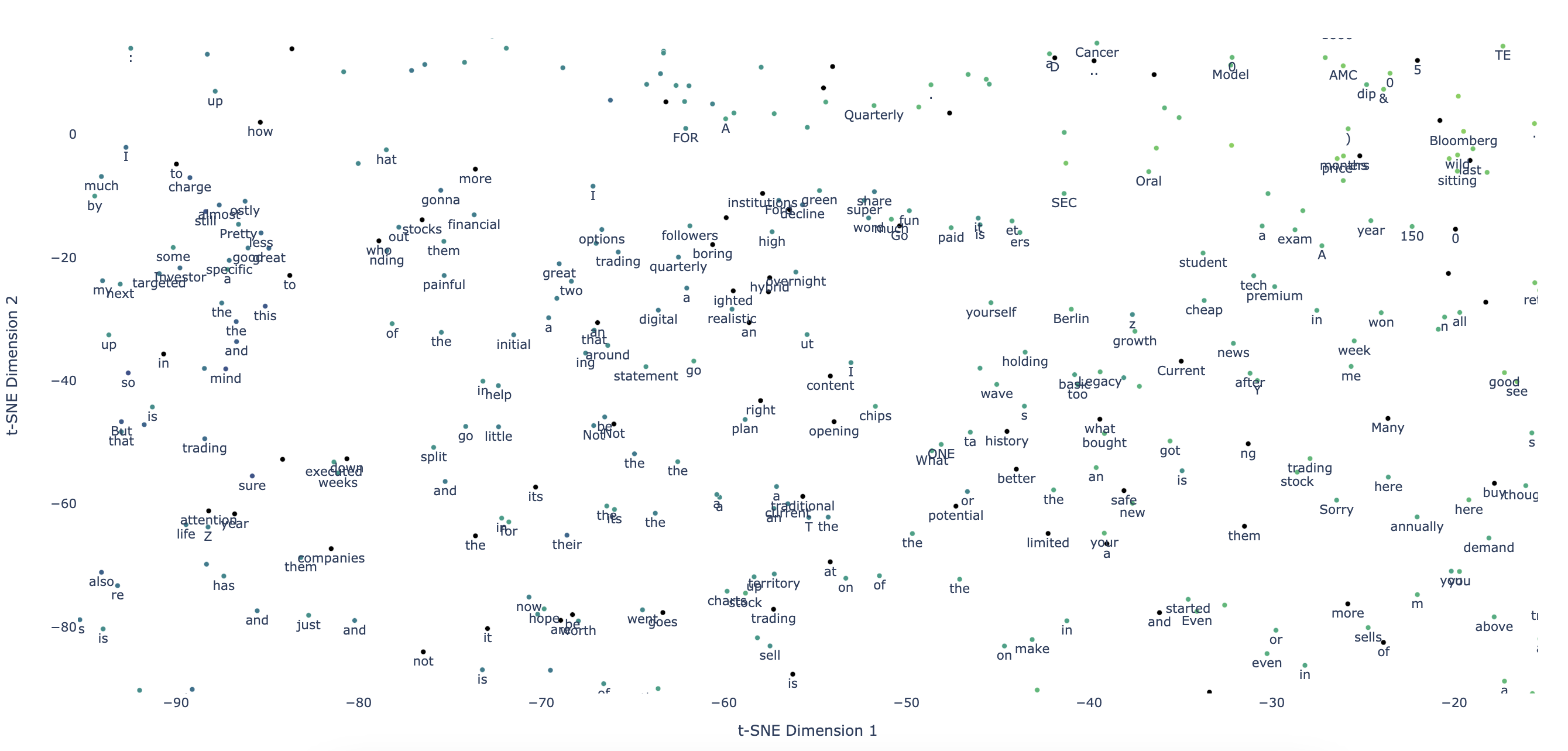
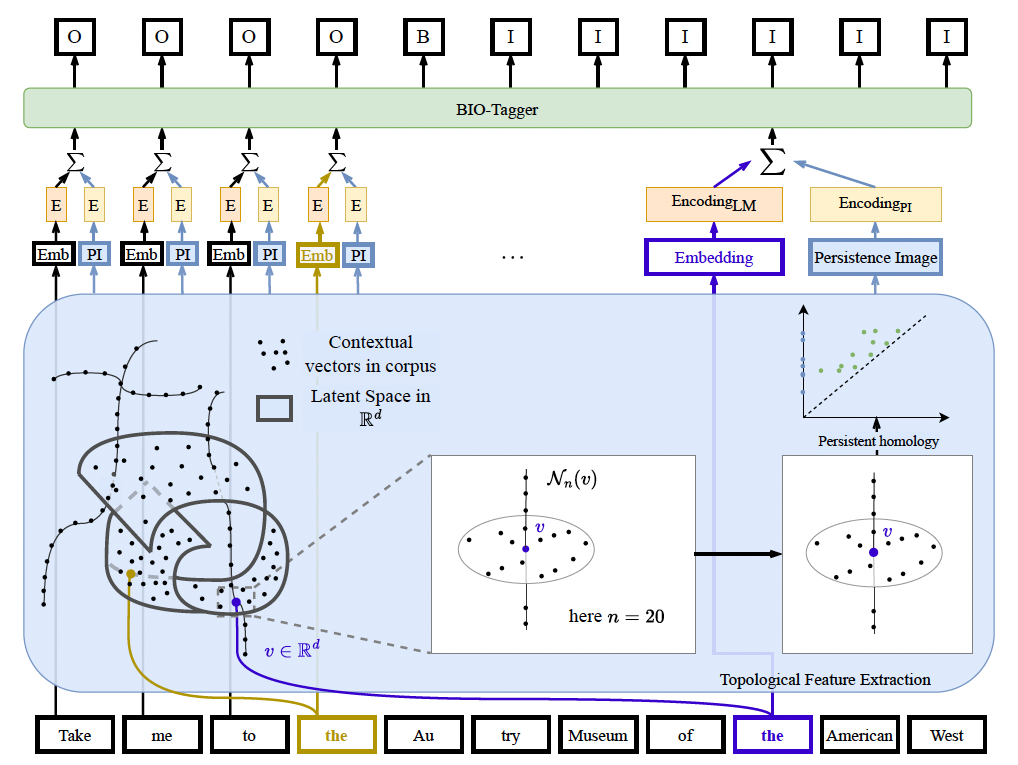
We show that contextual topological features derived from a given text corpus can be used to enhance the performance of a tagging task on dialogue data.
Nominated for Best Paper Award at SIGDIAL 2024Proceedings of the 25th Meeting of the Special Interest Group on Discourse and Dialogue (SIGDIAL 2024), Kyoto University, Japandoi:10.18653/v1/2024.sigdial-1.31arXiv:2408.03706Public Codebase
 ORCID
ORCID